| Horn type | Reflectance | Diameter function |
| parabolic | 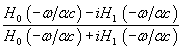 |
|
| conical | ||
| exponential | 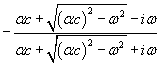 |
Reflectance evaluated at x = 0, and diameter function for parabolic, conical and exponential horns. Hν is the Hankel function of the first kind and order ν, c is the speed of sound, and α is a parameter used to achieve a desired area expansion.
| Horn type | Reflectance | Diameter function |
| parabolic | 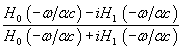 |
|
| conical | ||
| exponential | 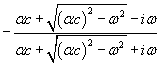 |
Reflectance in the frequency-domain R(0,2π f). The reflectance functions were obtained from theoretical equations presented in the Table above
Reflectance in the time domain. The inverse Fourier transforms of frequency-domain reflectance were multiplied by the sampling rate to display values that are independent of sampling rate
Horn diameter inverse solution (solid lines) compared with true values (dashed lines), which were calculated from the expressions listed in Table above. The curves in this figure represent horn diameter D(x) as a function of axial distance ( x ). In the selected examples, the diameter is 1 cm at x = 0 and expands to make the cross-sectional area A = 10 cm2 for all horn shapes at x = 10 cm.
![]() Boys
Town
National
Research Hospital
Boys
Town
National
Research Hospital
Communication Engineering Laboratory